bayesian hw 3

chapter 3

第一题

a

临床试验的例子，

安慰剂服从\(Y～N(\mu,\sigma^2) ,i=1,..,n\) ,

实验药服从\(N～N(\mu + \delta,\sigma^2),i=1+n,..,n+m\)

b

c

# 先验参数
n <- m <- 50
mu <- 10
delta <- 1
sigma <- 2

# 模拟数据
y1 <- rnorm(n,mu,sigma)
y2 <- rnorm(m,mu+delta,sigma)
y <- c(y1,y2)

# Gibbs
set.seed(2024)
S<-10000
PHI<-matrix(nrow=S,ncol=3)
PHI[1,]<-phi<-c(0, 0, 4) # sigma2

## Gibbs sampling algorithm
for(s in 2:S) {

# generate a new mu value from its full conditional
mu_n<- n*100*100*mean(y1)/(4+n*100*100)
s2_n<- (100*100*4)/(4+n*100*100)
phi[1]<-rnorm(1, mu_n, sqrt(s2_n) )

# generate a new delta value from its full conditional
# delta_m<-  ( m*100*100*mean(y2)/(4+m*100*100))-( n*100*100*mean(y1)/(4+n*100*100))
delta_m<-  (100*100*sum(y2-mu_n)/(4+m*100*100))

s2_m<- (100*100*4)/(4+m*100*100)
phi[2]<-rnorm(1, delta_m, sqrt(s2_m) )

# generate a new sigma^2 value from its full conditional
a <- 0.01+(m+n)*0.5
b <-0.01+(m+n)*0.5*((sum((y-mean(y))^2)/(m+n))+((mean(y)-(n*mu+m*(mu+delta))/(m+n))^2))
phi[3]<- 1/rgamma(1, a, b)
PHI[s,]<-phi         }

plot(density(PHI[,1]),main='mu')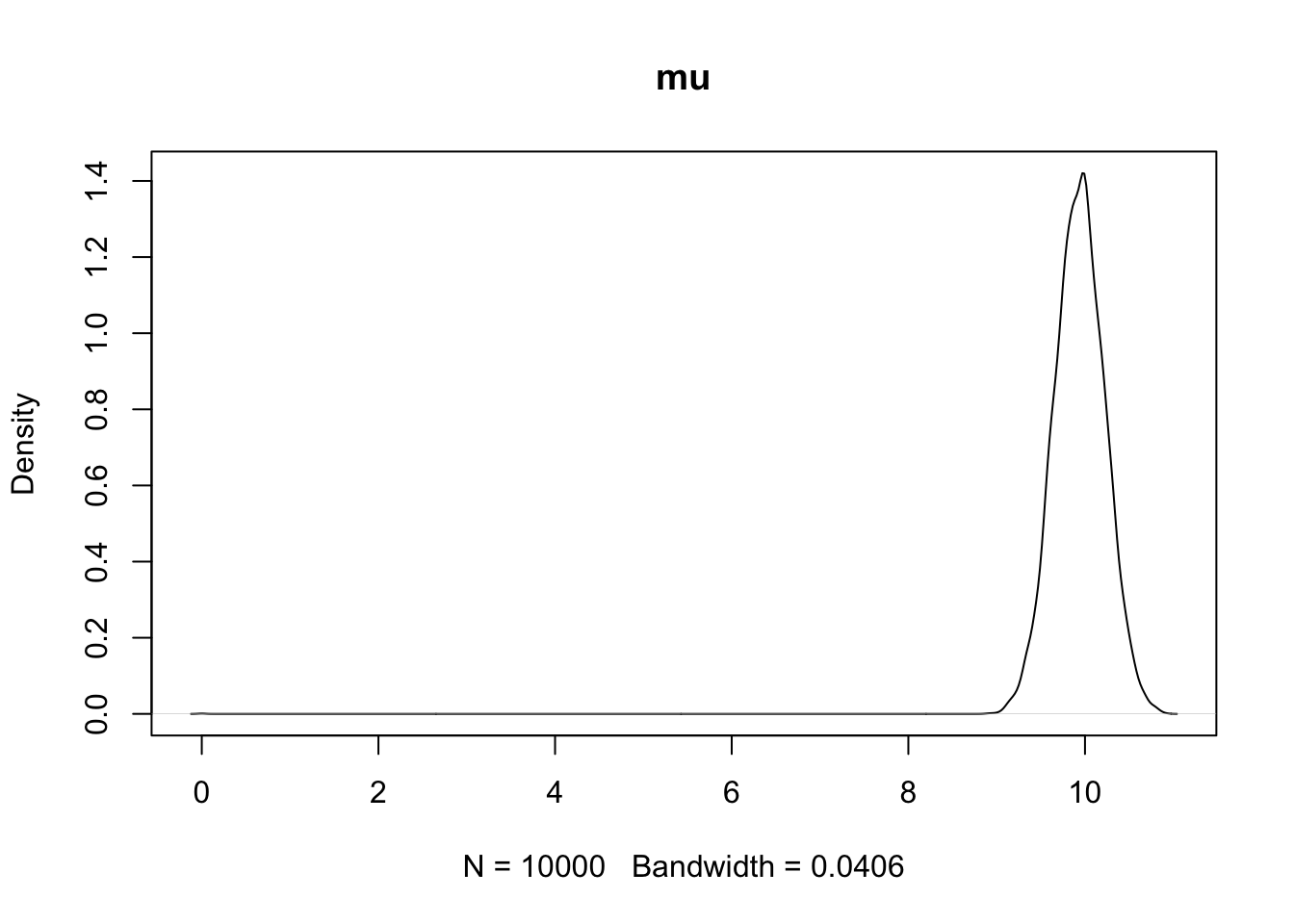

plot(density(PHI[,2]),main='delta')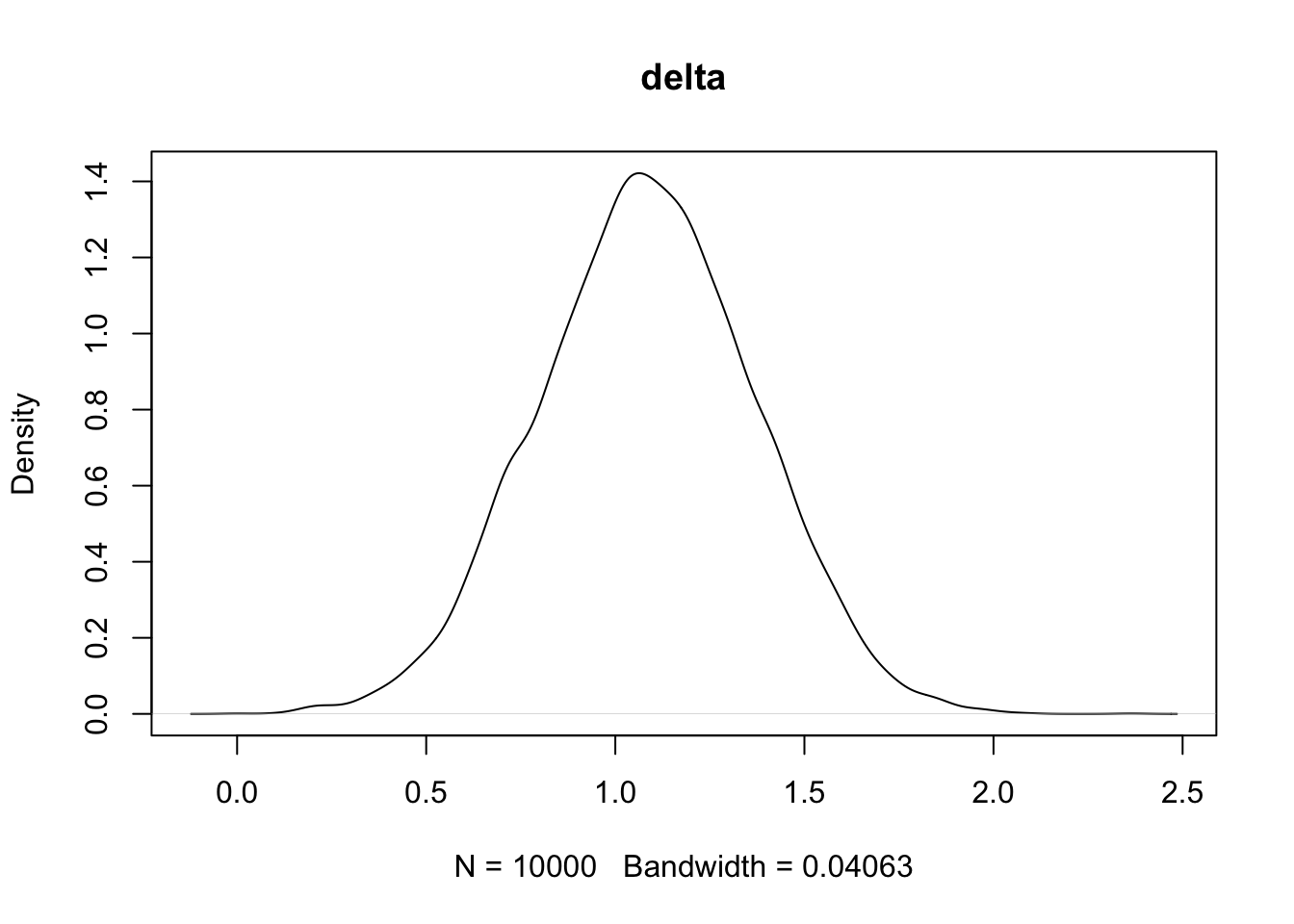

plot(density(PHI[,3]),main='sigma2')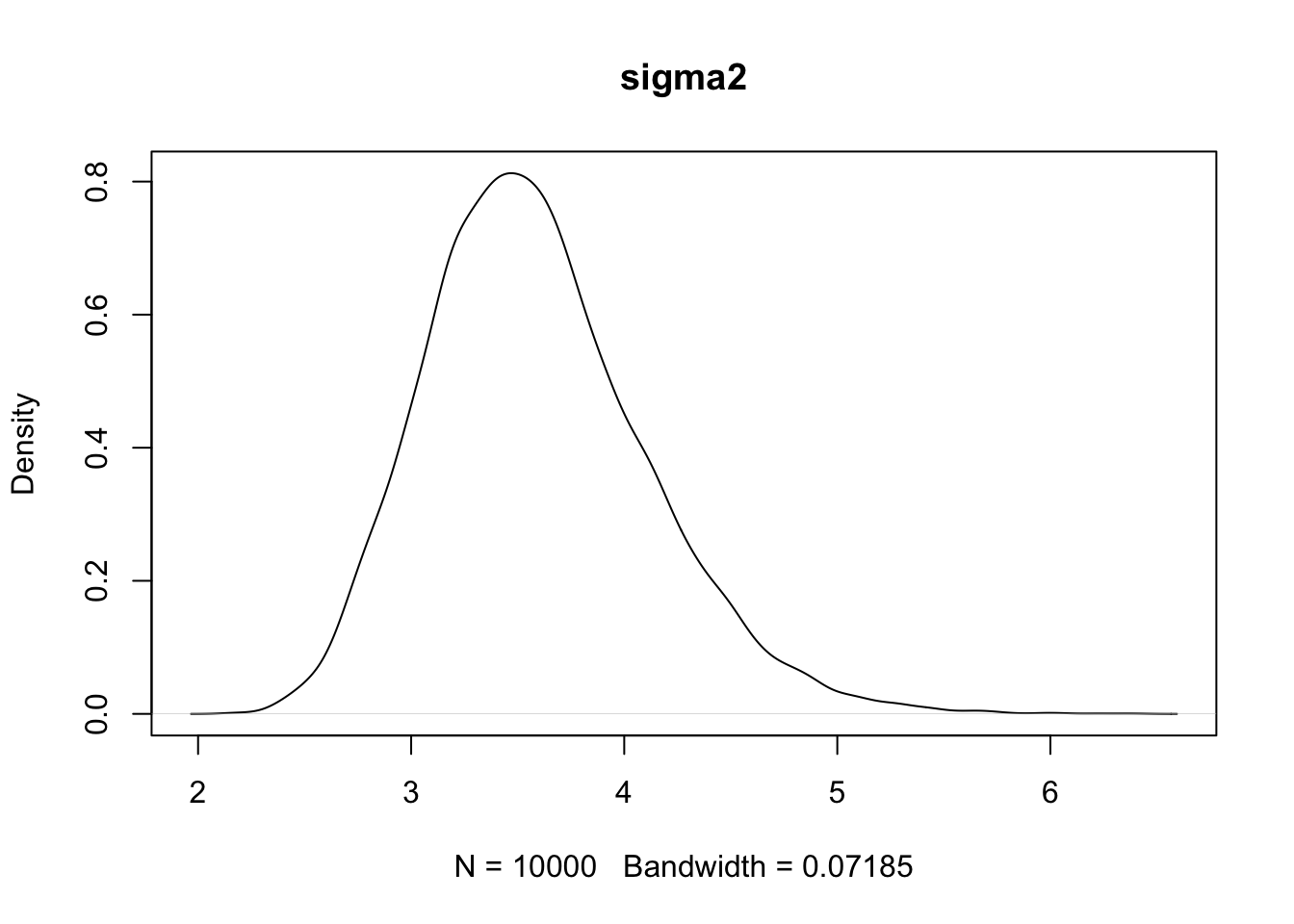

d

library('rjags')

Loading required package: coda

Linked to JAGS 4.3.2

Loaded modules: basemod,bugs

library("coda")


model_code <- "
model {

  for (i in 1:n) {
    Y[i] ~ dnorm(mu, 1/sigma2)
  }
  
  for (i in (n+1):(n+m)) {
    Y[i] ~ dnorm(mu + delta, 1/sigma2)
  }

  mu ~ dnorm(0, 1/10000)
  delta ~ dnorm(0, 1/10000)
  tau ~ dgamma(0.01, 0.01)
  sigma2 =  1/tau
}
"

n <- 50
m <- 50
mu_n <- 10
delta <- 1
sigma <- 2

set.seed(2024)
Y <- c(rnorm(n, mu_n, sigma), rnorm(m, mu_n + delta, sigma))

data_list <- list(Y = Y, n = n, m = m)



model <- jags.model(textConnection(model_code), data = data_list, n.chains = 3, n.adapt = 5000)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 100
   Unobserved stochastic nodes: 3
   Total graph size: 113

Initializing model

# 运行 MCMC 采样
update(model, 5000) # Burn-in阶段
samples <- coda.samples(model, variable.names = c("mu", "delta", "sigma2"), n.iter = 5000)

plot(samples)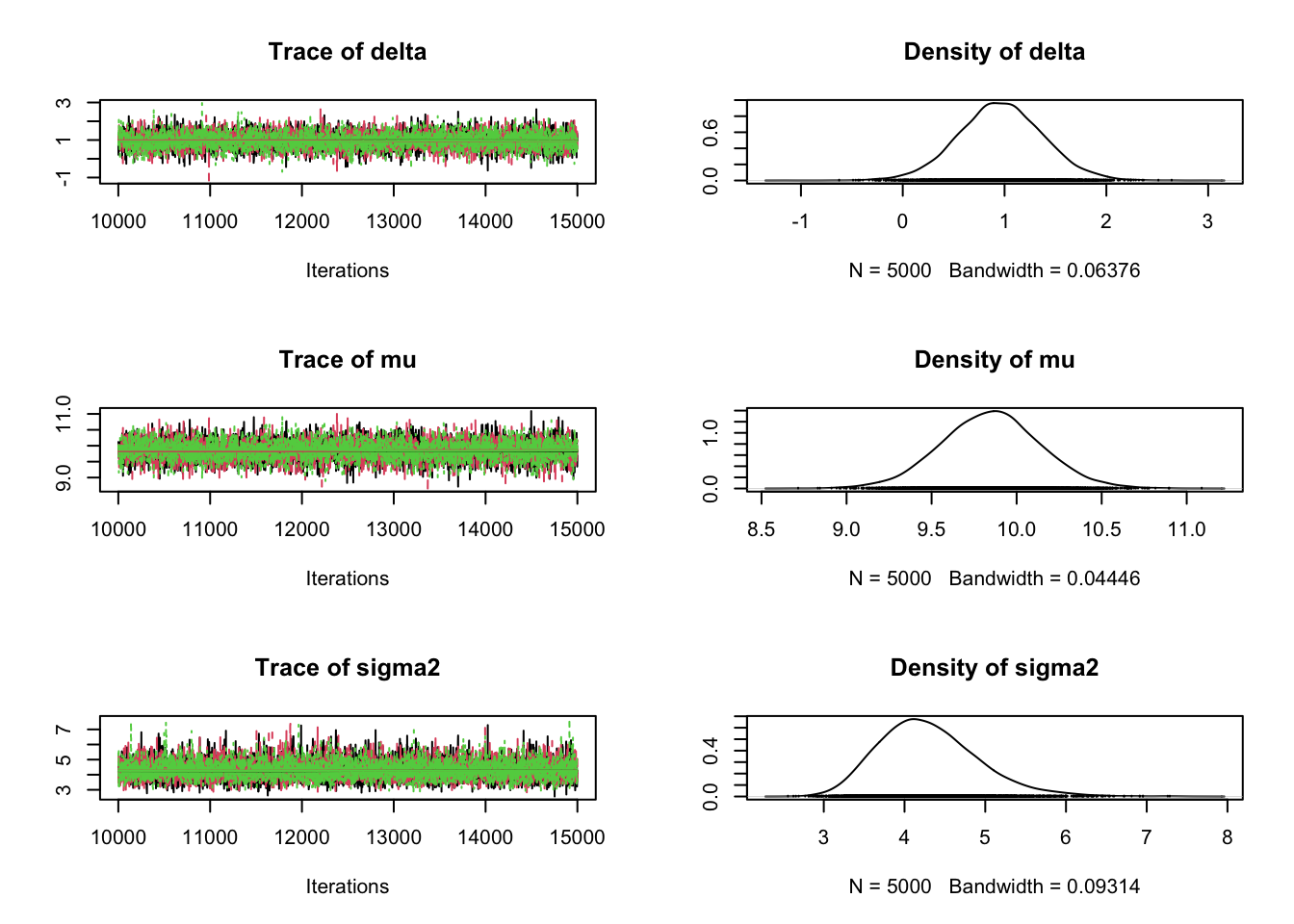

e

# gelman.diag(samples)

# 自相关
acf(as.matrix(samples)[, "mu"])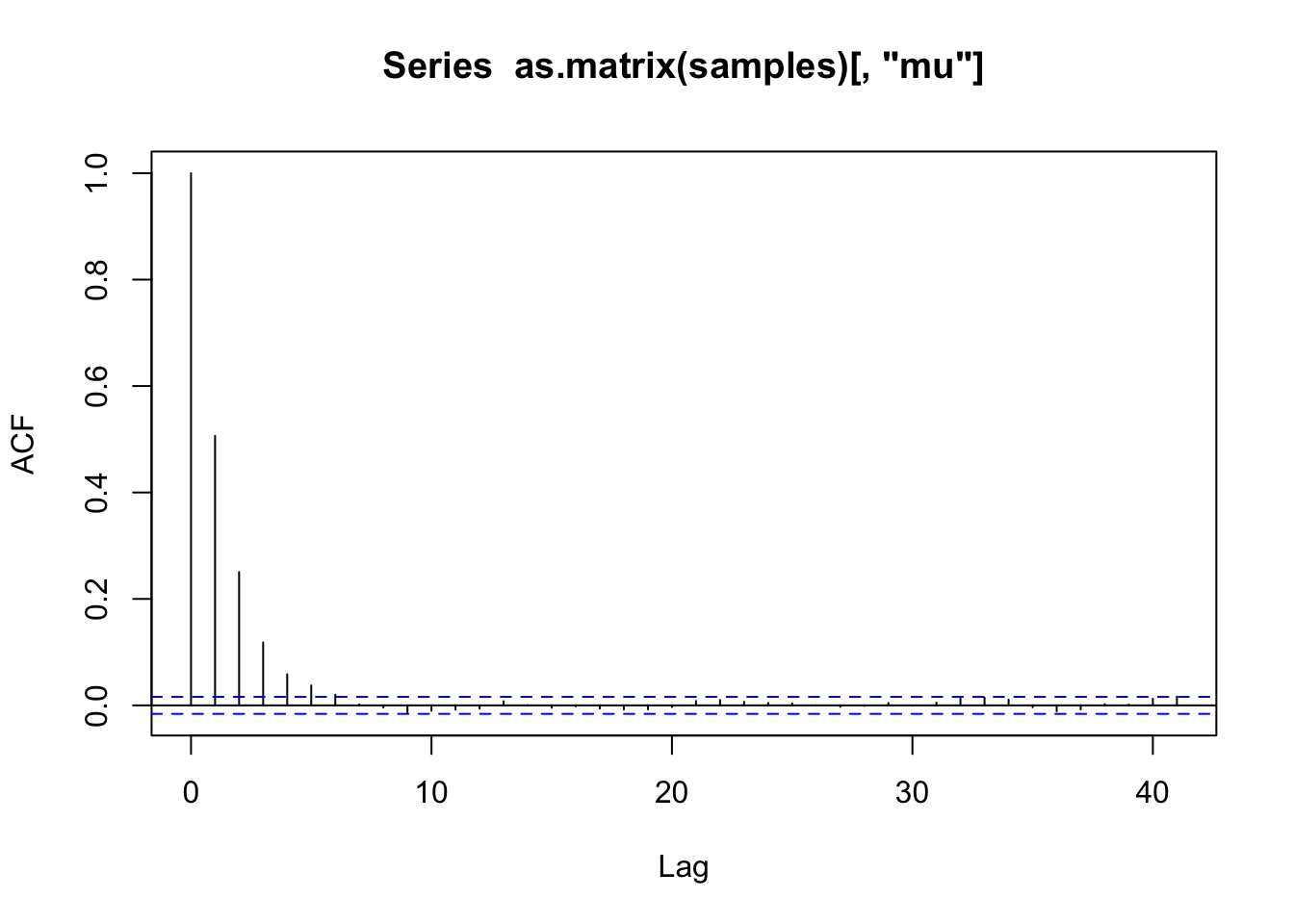

acf(as.matrix(samples)[, "delta"])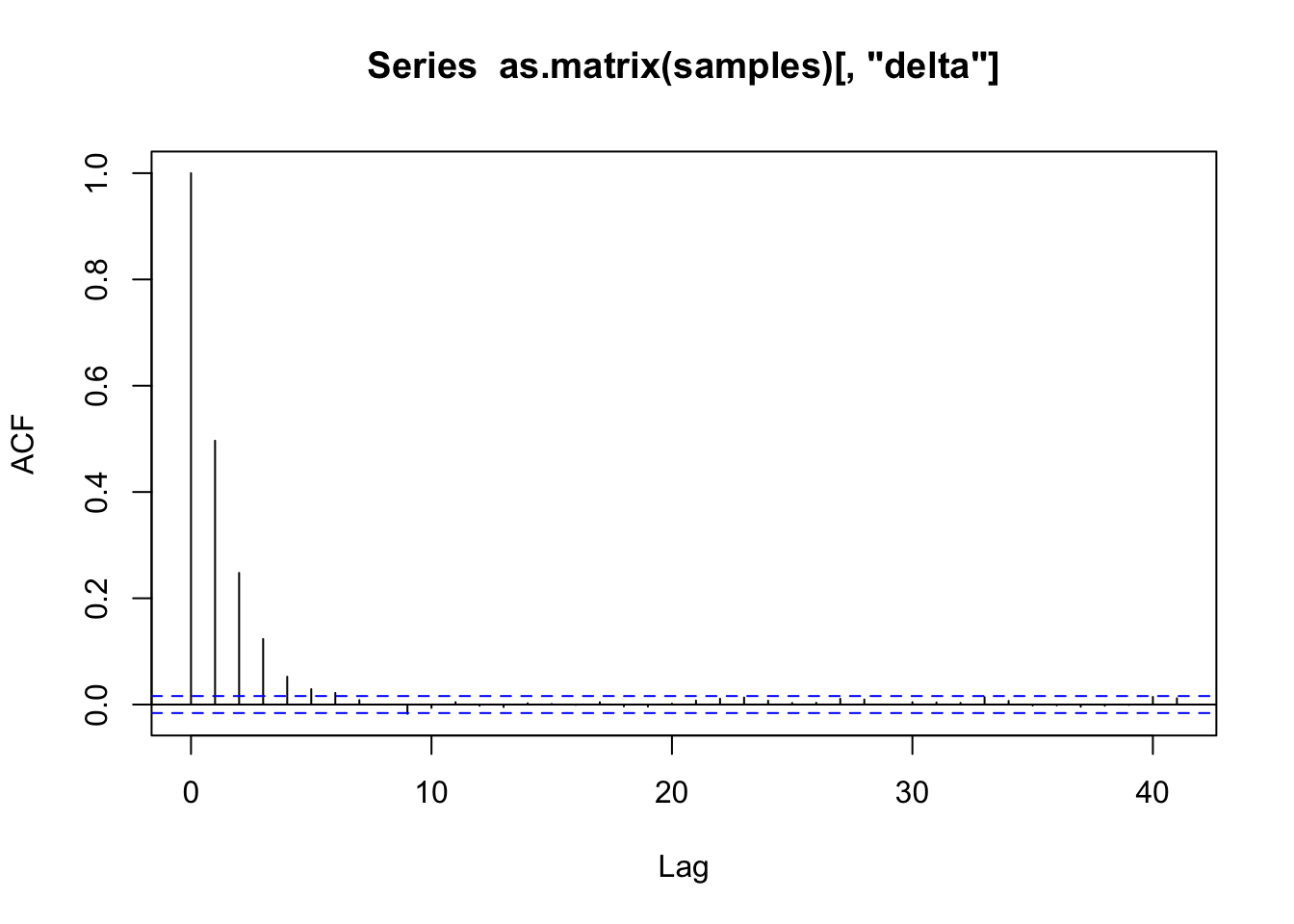

acf(as.matrix(samples)[, "sigma2"])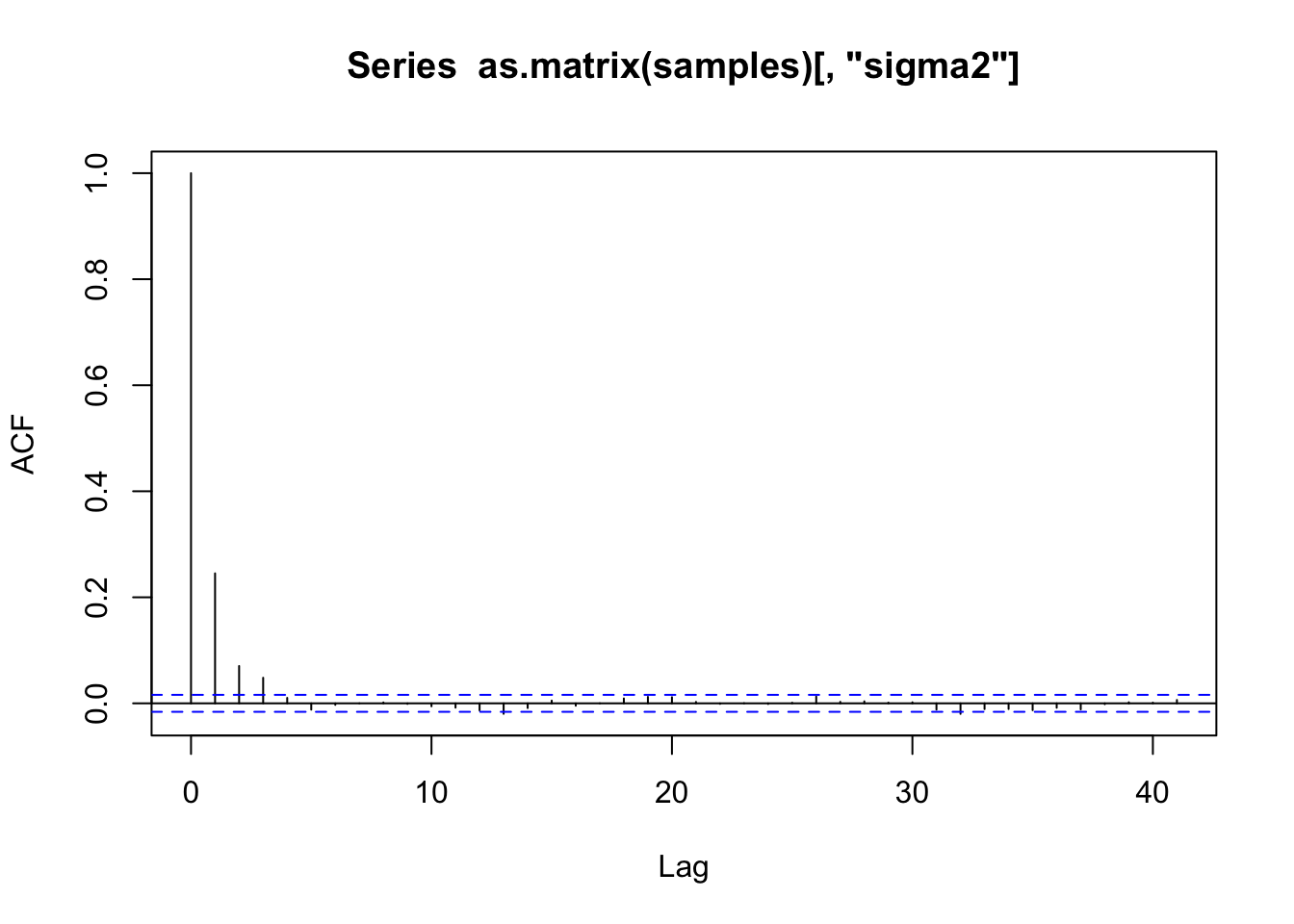

# 有效样本量
effectiveSize(samples)

   delta       mu   sigma2 
5249.571 5011.195 8744.733 

第二题

a

首先共轭 beta分布对于概率\(\theta\)来说是常规的先验分布设置手段。因为其足够灵活并且在0，1之间变化; 其次，这样设置还有现实意义的解释，即beta分布中，a=命中多少个，b=未能命中的个数; 最后，添加了一个exp(m)这样一个调节的量，表示在常规命中率的基础上引入变化 exp（m）等于试验总次数取exp保持其为正，exp(m)q/(a+b)=成功的概率刚好等于q，表示平时命中率用到了样本信息

set.seed(2024)
theta_i <- c(0.845, 0.847, 0.880, 0.674, 0.909, 0.898, 0.770, 0.801, 0.802, 0.875)
m_samples <- rnorm(1000, mean = 0, sd = 10)

probabilities <- numeric(10000)

for (i in 1:1000) {
  m <- m_samples[i] 

  for (j in 1:10) {
    shape1 <- exp(m) * theta_i[j]       
    shape2 <- exp(m) * (1 - theta_i[j]) 
    probability <- rbeta(1, shape1, shape2)
    probabilities[(i - 1) * 10 + j] <- probability
  }
}


hist(probabilities,probability = TRUE)
lines(density(probabilities), col = "red", lwd = 2)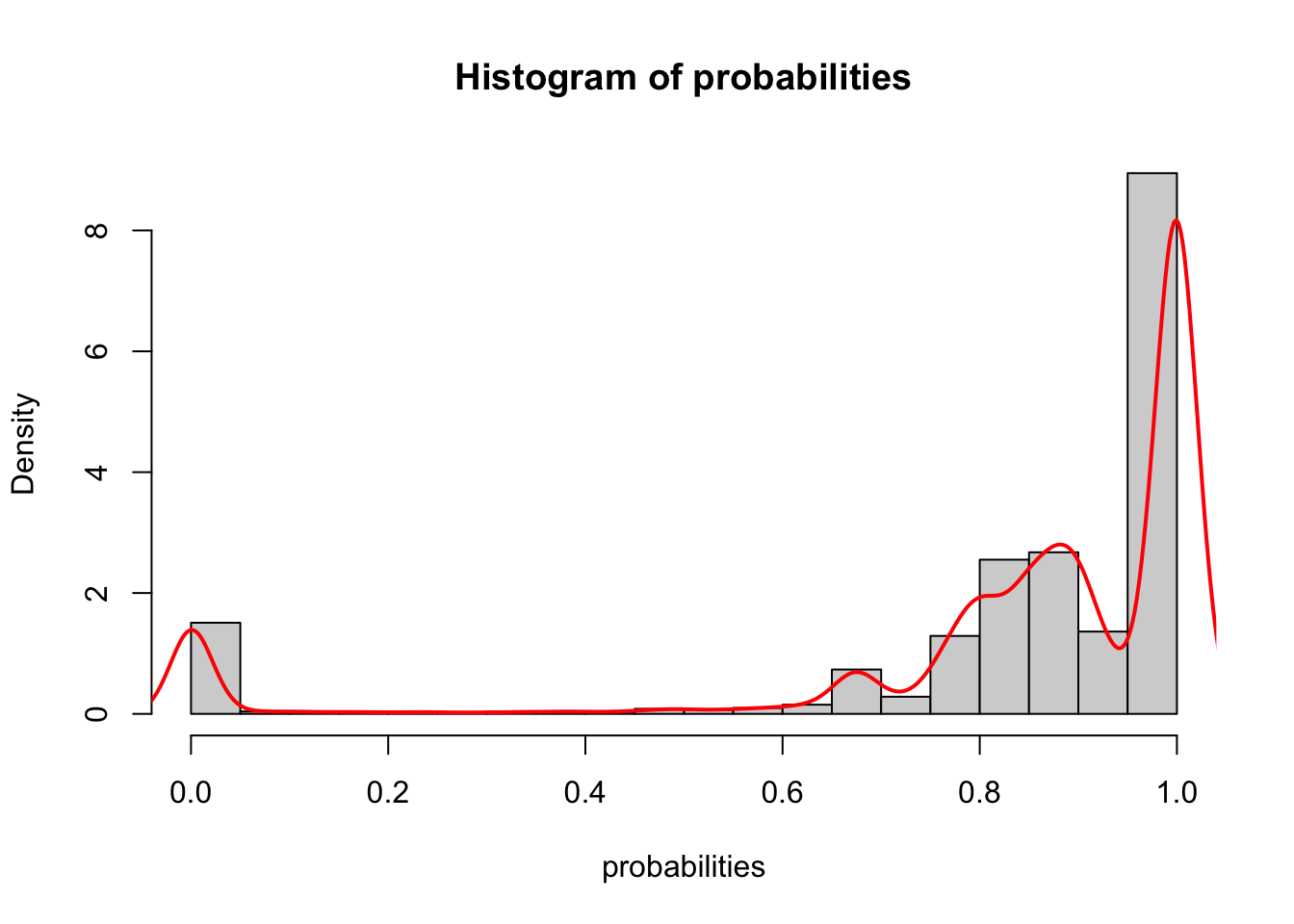 

b

m引入了不确定性 exp(m)先验样本量

c

后验：

\[ beta(y+exp(m)*q_{i} , exp(m)*(1-q_i)+n-y) \]

d

### data input
q <- c(0.845,0.847,0.880,0.674,0.909,0.898,0.770,0.801,0.801,0.875)
y <- c(64,72,55,27,75,24,28,66,40,13)
n <- c(75,95,63,39,83,26,41,82,54,16)

### prior
mu_m <- 0
tau_m_2 <- 10

### Metropolis + Gibbs sampling
set.seed(1)
S<-10000
PHI<-matrix(nrow=S,ncol=length(n)+1)
PHI[1,]<-phi<-c(q, 0)

# help function for Metropolis step
log_m <- function(theta,m){
  like  <- sum(dbeta(theta,exp(m)*q,exp(m)*(1-q),log=TRUE))
  prior <- dnorm(m,mu_m,sqrt(tau_m_2),log=TRUE)
  return(like+prior)}

# proposal candidate standard deviation
can_sd <- 2

# monitoring acceptance rate
acs <- 0

for(s in 2:S){
  
  # Metropolis for m
  can    <- rnorm(1,phi[11],can_sd)
  logR   <- log_m(phi[1:10],can)-
    log_m(phi[1:10],phi[11])
  if(log(runif(1))<logR){
    phi[11] <- can; acs <- acs+1 
  }
  
  # Gibbs for theta
  for (i in 1:length(n) ) {
    phi[i] <- rbeta(1, exp(phi[11])*q[i]+y[i],exp(phi[11])*(1-q[i])+n[i]-y[i] )
  }
  
  PHI[s,] <- phi
}

acs/S

[1] 0.2802

# 目标接受率
# 
# • 0.2 到 0.5：
# 这是 Metropolis 算法的常见推荐范围。一般来说，较低的接受率可能意味着步长太大，
# 导致大量候选值被拒绝；较高的接受率可能意味着步长太小，导致缺乏足够的探索。适中的接受率通常是最理想的。
# 
# 如何调整接受率？
# 
# • 调整候选分布的标准差（can_sd）：
# 如果接受率较低，可以尝试增大 can_sd，从而让候选值更有可能接受。
# 如果接受率较高，可以尝试减小 can_sd，以避免候选值过于接近当前值，从而增加采样的多样性。

# 在Metropolis-Hastings算法中，can_sd 是用来生成候选值（candidate values）的标准差，它决定了每次提议的新候选点（can）与当前点（phi[11]）之间的距离。
# 这是一个非常重要的超参数，它影响了算法的收敛速度和效率。具体来说，它决定了提议的新参数值的“步长”，即每次更新时的幅度

apply(PHI[5000:10000, ], 2, 
      function(x) quantile(x,c(0.05,0.5,0.95)))

         [,1]      [,2]      [,3]      [,4]      [,5]      [,6]      [,7]
5%  0.8104456 0.7615902 0.8440256 0.6295148 0.8784673 0.8660099 0.6932799
50% 0.8461988 0.8272104 0.8800869 0.6763726 0.9087521 0.9002698 0.7609262
95% 0.8804987 0.8538625 0.9106061 0.7280584 0.9333923 0.9352580 0.7931326
         [,8]      [,9]     [,10]    [,11]
5%  0.7627631 0.7299636 0.8242682 3.746227
50% 0.8018394 0.7935902 0.8730267 5.535272
95% 0.8407672 0.8249428 0.9063106 8.804084

e

library(rjags)
library(coda)

model_string <- "
model {


  for (i in 1:n_players) {

    clutch_makes[i] ~ dbin(theta[i], clutch_attempts[i])

    theta[i] ~ dbeta(alpha[i], beta[i])

    alpha[i] <- exp(m) * theta_i[i]
    beta[i] <- exp(m) * (1 - theta_i[i]) 
  }
   m ~ dnorm(0,1/10)
}
"

theta_i <- c(0.845, 0.847, 0.880, 0.674, 0.909, 0.898, 0.770, 0.801, 0.802, 0.875)
clutch_makes <- c(64, 72, 55, 27, 75, 24, 28, 66, 40, 13)
clutch_attempts <- c(75, 95, 63, 39, 83, 26, 41, 82, 54, 16)
n_players <- length(theta_i)


data_jags <- list(
  theta_i = theta_i,         
  clutch_makes = clutch_makes,
  clutch_attempts = clutch_attempts,
  n_players = n_players
)



model <- jags.model(textConnection(model_string), data = data_jags)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 10
   Unobserved stochastic nodes: 11
   Total graph size: 77

Initializing model

update(model, 10000)

n_samples <- 10000
samples <- coda.samples(model, variable.names = c('theta','m'), n.iter = n_samples)

# plot(samples)
summary(samples)

Iterations = 11001:21000
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 10000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

            Mean      SD  Naive SE Time-series SE
m         5.6291 1.38623 0.0138623      0.0745150
theta[1]  0.8467 0.02182 0.0002182      0.0003428
theta[2]  0.8191 0.02868 0.0002868      0.0009502
theta[3]  0.8780 0.02128 0.0002128      0.0003354
theta[4]  0.6782 0.03142 0.0003142      0.0004753
theta[5]  0.9073 0.01722 0.0001722      0.0002340
theta[6]  0.9015 0.02116 0.0002116      0.0003171
theta[7]  0.7543 0.03338 0.0003338      0.0007306
theta[8]  0.8027 0.02357 0.0002357      0.0003387
theta[9]  0.7879 0.02918 0.0002918      0.0006779
theta[10] 0.8692 0.02708 0.0002708      0.0004883

2. Quantiles for each variable:

            2.5%    25%    50%    75%  97.5%
m         3.3911 4.6504 5.4322 6.4312 8.9092
theta[1]  0.8014 0.8354 0.8465 0.8586 0.8909
theta[2]  0.7512 0.8025 0.8253 0.8410 0.8586
theta[3]  0.8285 0.8678 0.8794 0.8901 0.9178
theta[4]  0.6167 0.6611 0.6764 0.6945 0.7472
theta[5]  0.8672 0.8985 0.9087 0.9174 0.9396
theta[6]  0.8573 0.8910 0.9007 0.9131 0.9464
theta[7]  0.6681 0.7393 0.7611 0.7744 0.8072
theta[8]  0.7519 0.7901 0.8027 0.8157 0.8516
theta[9]  0.7171 0.7736 0.7934 0.8058 0.8358
theta[10] 0.8034 0.8578 0.8725 0.8837 0.9172

f

自己的代码需要推导后验分布或者用更复杂的M-H方法

g

effectiveSize(samples)

        m  theta[1]  theta[2]  theta[3]  theta[4]  theta[5]  theta[6]  theta[7] 
 346.0851 4050.9905  911.1794 4024.1671 4369.1464 5413.8186 4454.2546 2087.0520 
 theta[8]  theta[9] theta[10] 
4842.3959 1852.5650 3074.5285 

第三题

a

library(MASS)
data(galaxies)
?galaxies
Y <- galaxies

n <- length(Y)

hist(Y,breaks=25)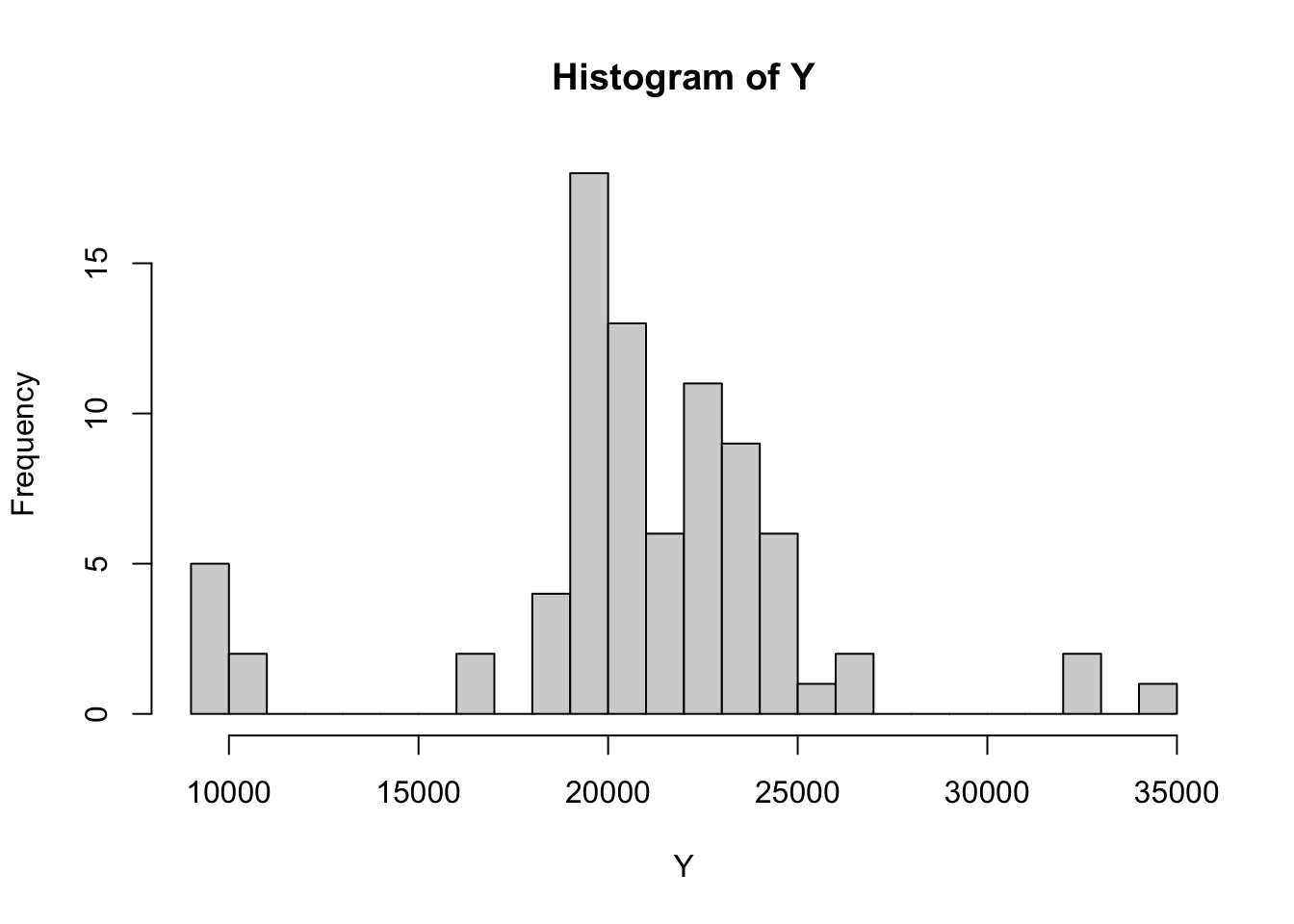

\(\mu=20000\)

\(\sigma=5000\)

\(k=15\)

b

library(rjags)
library(coda)

model_string <- "
model {
  for (i in 1:s) {
    Y[i] ~ dt(mu, tau, k)
  }
  mu ~ dnorm(0, 1/10000^2)
  tau ~ dgamma(0.01, 0.01)
  k ~ dunif(1, 30)
}
"

data_jags <- list(Y =galaxies, s = length(galaxies))

# 设置初始值
init_values <- list(
  list(mu = 0, tau = 100, k = 15)
)

# 创建模型
model <- jags.model(textConnection(model_string), data = data_jags, inits = init_values, n.chains = 1)

Compiling model graph
   Resolving undeclared variables
   Allocating nodes
Graph information:
   Observed stochastic nodes: 82
   Unobserved stochastic nodes: 3
   Total graph size: 94

Initializing model

# 更新模型
update(model, 10000)

# 采样
n_samples <- 10000
samples <- coda.samples(model, variable.names = c("mu", "tau", "k"), n.iter = n_samples)

# 绘制轨迹图
plot(samples)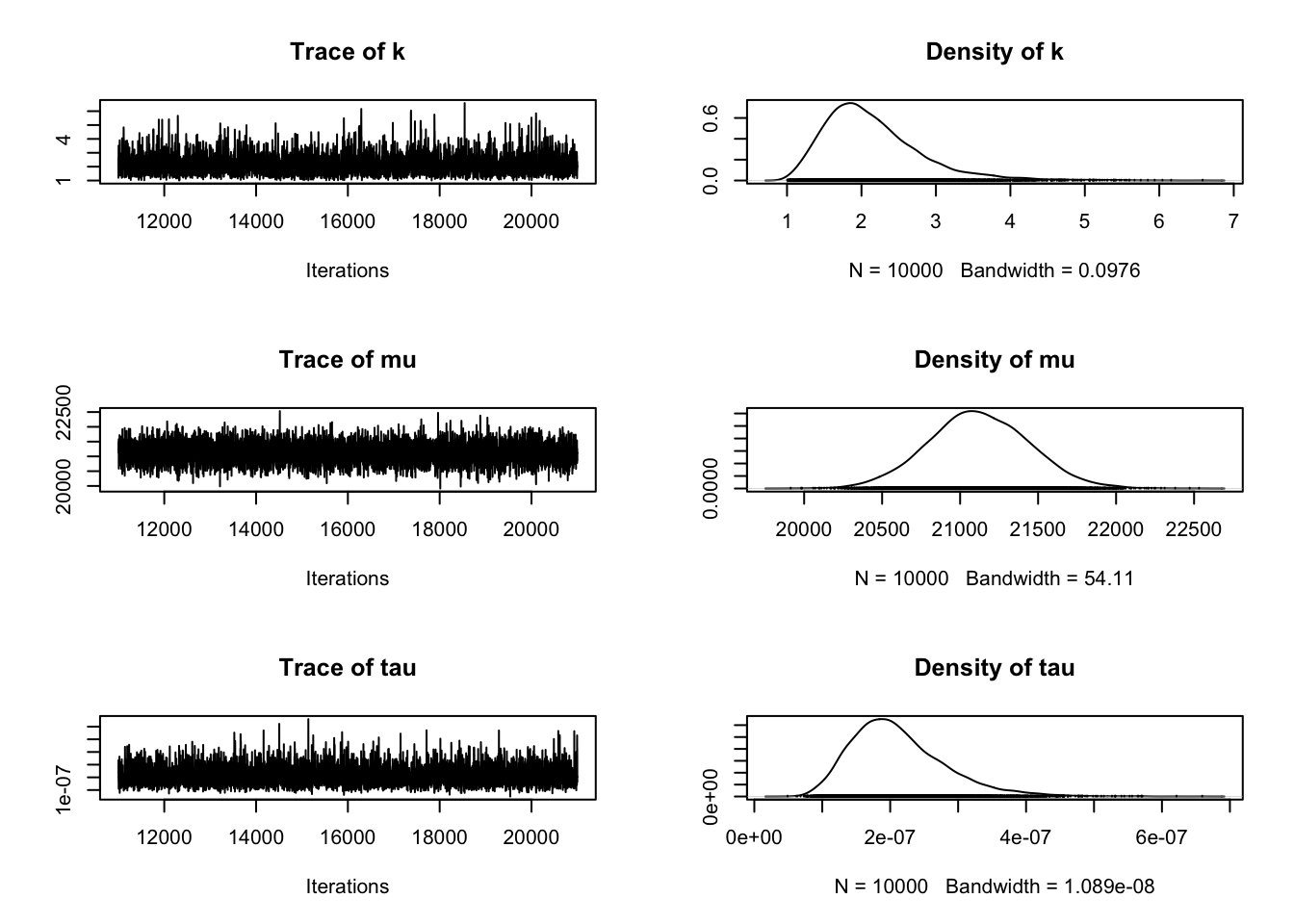

c

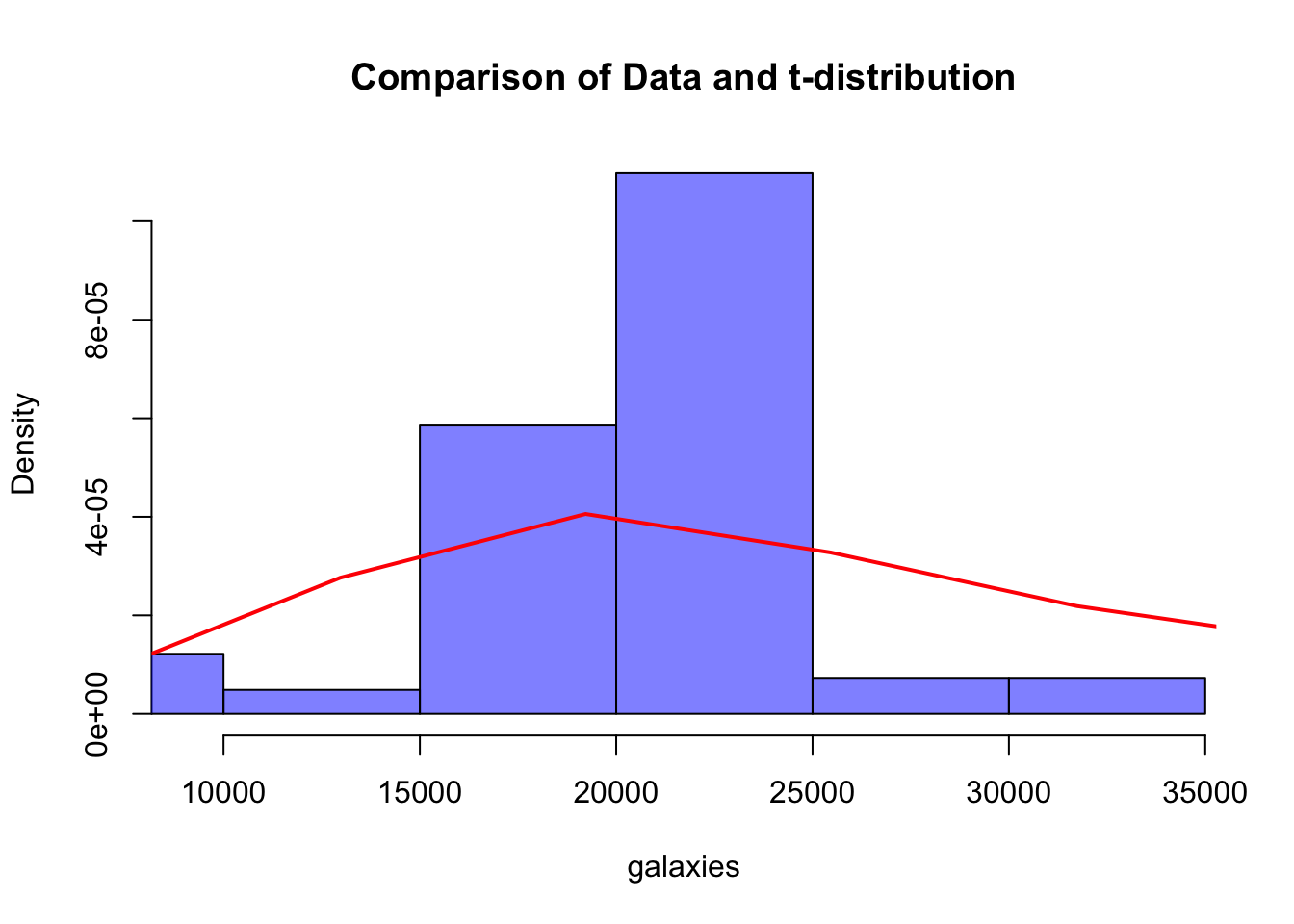
posterior_means <- apply(as.matrix(samples), 2, mean)

# 从后验均值计算t分布
mu_posterior <- posterior_means["mu"]
sigma_posterior <- 1/sqrt(posterior_means["tau"])
k_posterior <- posterior_means["k"]

# 生成t分布的随机样本
t_dist_samples <- rt(10000, df = k_posterior, ncp = mu_posterior)

# 绘制观察数据和t分布的对比图
hist(galaxies, probability = TRUE, col = rgb(0, 0, 1, 0.5), main = "Comparison of Data and t-distribution", xlim = c(min(galaxies), max(galaxies)))
lines(density(t_dist_samples), col = "red", lwd = 2,xlim=c(10000,35000))